SubdivNet阅读笔记

SubDivNet 学习笔记

这篇文章主要讲述的是如何将卷积神经网络从图像迁移到三维模型中, 从而实现通过使用经典的神经网络模型(如resNet等)实现对三维模型的分类，分割等任务。

相关术语

1. Loop Subdivsion Connectivity

如果一个网格能够用一个更粗糙的网格通过Loop细分得到，则称这个网格拥有Loop Subdivsion Connectivity

2. Loop Subdivsion sequence connectivity

如果有一个网格序列$\{M_0, M_1, \ldots , M_n\}$，满足以下两个条件，

1. 对于序列中的任意一个网格$M_i (i \neq 0)$都具有Loop Subdivsion Connectivity
2. 对于任意一个网格$M_i(0 \le i < n)$, 该网格中的所有点都存在于下一个网格中$M_{i + 1}$中

则称这样的一个网格序列具有Loop Subdivsion Sequence Connectivity

网格remesh

SubdivNet方法中由于涉及到池化和超采样两个部分, 所以需要确保当网格变稀疏或者变稠密后, 改变后的网格相较于原始的网格任能够保证一定的联系, 这样能够方便后继的池化和超采样。

remesh的方法参考自论文MAPS: multiresolution adaptive parameterization of surfaces, 其主要思想是先将网格简化, 生成一个网格序列$\{M_0, M_1, \ldots, M_n\}$(其中$M_0$为最粗糙的网格, $M_n$为原始网格),并找到原始网格到最粗糙网格的双射$\Pi$, 之后通过在$M_0$上做中点细分并映射回$M_n$完成网格remesh.

网格简化

假定现在有一个网格$M_i$, 目标是寻找一个简化的网格$M_{i-1}$, 可以按照以下步骤寻找

1. 算每一个点的权重

通过以下公式计算网格$M_i$中每一个点的权重$W(\lambda, i)$

$$W(\lambda, i) = \lambda \frac{a(i)}{\max_{p_i \in P^l}a(i)} + (1 - \lambda) \frac{\kappa(i)}{\max_{p_i \in P^l}\kappa(i)}$$

其中:

$a(i)$表示在第$i$个点的1领域三角面片的面积之和。

$\kappa(i)$表示在第$i$个点上的曲率, 由在该点的两个主曲率($\kappa_1, \kappa_2$)相加得到, 即$\kappa(i) = \kappa_1(i) + \kappa_2(i)$。

在论文中, $\lambda$取值为0.5。

2. 去除最大独立点集

找到网格$M_i$中未标记的权重最小的点, 并标记该点为可去除点, 同时标记其所有邻居点为不可移除点, 循环该过程, 直到标记完所有点, 如下图所示, 其中黑点为去除点。

对于点击中的每一个点, 在网格中去除掉该点和与其直接相连的边。

在实际操作的时候, 并不一定会去除掉全部的点, 例如, 假设现在需要保证在下一个网格中总共有$i$个点, 而现在总共有$n$个点, 则只需要删除$n-i$的点。这一点在之后设计网络的时候尤为重要, 因为我们需要保证网络有相同个数的输出以便分类。

3. 在去除点及其1领域附近展开曲面, 并重新三角化

假设映射$z^a$表示曲面到平面的映射, 序列$\{j_0, j_1, \ldots, j_K\}$表示点$i$的1领域点, 且面$\{j_k, i, j_{k+1}\}$是原曲面(移除点之前)的一个三角面片, 用复数$\mu_i(p_{j_k}) = u + iv$表示点$j_k$映射到平面中的位置, 其中$u, v$表示点$j_k$在平面中的坐标, $p_{j_k}$表示点${j_k}$的三维坐标。对于被去除的点, 其坐标记为$(0, 0)$.

使用如下公式计算$\mu_i(p_{j_k})$

$$\begin{cases} \mu_i(p_{j_k}) = r_k^a \exp(i \theta_k a) \\ a = 2 \pi / \theta_{K_i} \\ \theta_k = \sum_{i=1}^k \angle(p_{j_{l-1}}, p_i, p_{j_l}) \\ r_k = \Vert p_i - p_{j_k} \Vert \\ \end{cases}$$

之后使用CDT方法在这个二维平面做三角化，并将连接关系映射回原网格即达成了对原网格的一次简化。

下图展示了一次重新三角化的过程

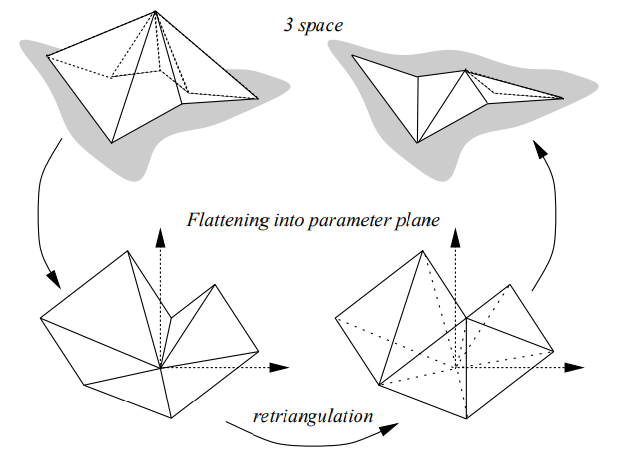
下图展示了对一个曲面多次简化的过程

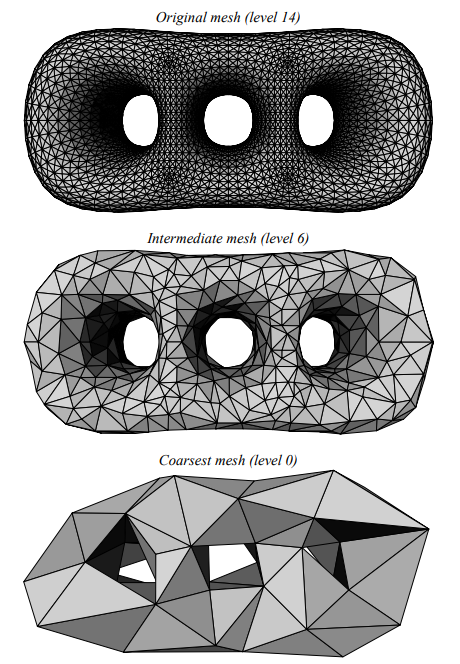
建立网格映射

为方便期间, 最粗糙网格也被称为基网格

令$\Pi$表示原始网格$K_L$到基网格$K_0$之间的双射, 即对于原始网格中的任意一个点$p$, 都能在$K_0$上找到一个点$p^0 = \Pi(p)$。

令$\Pi^l$表示原始网格$K_L$到第$l$层$K_l$网格之间的双射, 则$\Pi^{l - 1}$可以用$\Pi^l$来表示, 具体方法如下

1. 如果点$i$在第$l$层和第$l-1$层网络中都存在, 则 $\Pi^{l-1}(p_i) = \Pi^{l}(p_i) = p_i$

2. 如果点$i$在第$l$层中存在, 但是在$l-1$层中被移除, 那么在三角化之后, 在第$l-1$层中一定存在一个三角面片$\{j, k, m\}$和重心坐标$\{\alpha, \beta, \gamma\}$, 使得$\mu_i(p_i) = \alpha \mu_i(p_j) + \beta \mu_i(p_k) + \gamma \mu_i(p_m)$, 即$\Pi^{l-1}(p_i) = \alpha p_j + \beta p_k + \gamma p_m$。如下图所示。

   

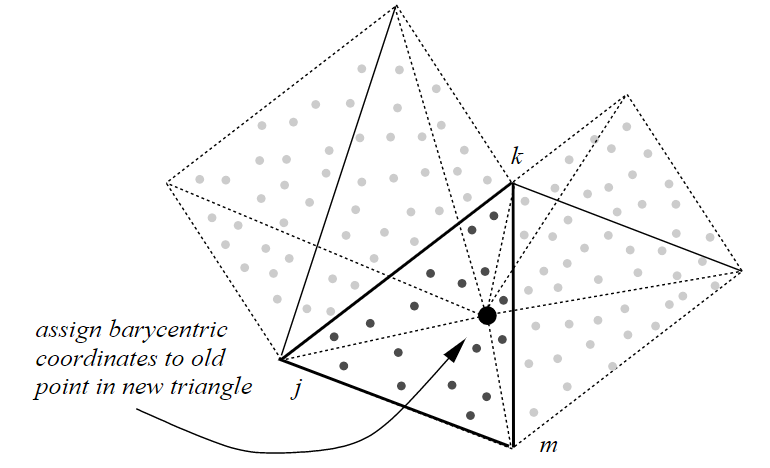
3. 如果点$i$在第$l$层和第$l-1$层中都不存在, 那么由2可知, $\Pi^{l}(p_i) = \alpha' p_{j'} +\beta' p_{k'} + \gamma' p_{m'}$。 其中, $\{j', k', m'\}$为第$l$层网格中的点

   1. 如果$\{j', k', m'\}$在第$l-1$层中依旧存在, 则$\Pi^{l-1}(p_i) = \Pi^{l}(p_i) = \alpha' p_{j'} +\beta' p_{k'} + \gamma' p_{m'}$

   2. 如果$\{j', k', m'\}$中存在点被移除, 由最大独立点集可知, 这三个点只可能被移除一个, 假设这个点是$j'$, 由2同理可得, 在第$l-1$层中一定存在一个三角面片$\{j, k, m\}$和重心坐标$\{\alpha, \beta, \gamma\}$, 使得$\mu_{j'}(p_{j'}) = \alpha \mu_{j'}(p_j) + \beta \mu_{j'}(p_k) + \gamma \mu_{j'}(p_m)$, 即$\Pi^{l-1}(p_i) = \alpha p_j + \beta p_k + \gamma p_m$

$\Pi$的作用是为了让原网格中的点都能够用基网格中的三个点来表示。

下图展示了原网格到基网格的映射

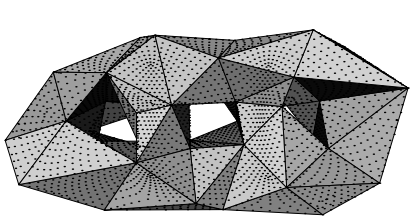
remeshing

remeshing的关键步骤是要建立一个反向映射$\Pi^{-1}$, 使得在最粗糙网格个上的点能够映射回原网格。 假设基网格上存在一点$q$, 而原平面上有一个三角面片$\{i, j, k\}$经过$\Pi$的映射之后正好包含了点$q$, 那么点$q$一定可以表示成如下形式

$$q = \alpha \Pi(p_i) + \beta \Pi(p_j) + \gamma \Pi(p_k)$$

则

$$\Pi^{-1}(q) = \alpha p_i + \beta p_j + \gamma p_k$$

对基网格上的面片进行三角细分, 之后再运用上面的公式将新的点反向映射到原网格上(去除原网格上的点), 即对于原始网格进行了remeshing

下图展示了remeshing的结果

MAPS的复现代码地址: https://github.com/45degree/MAPS

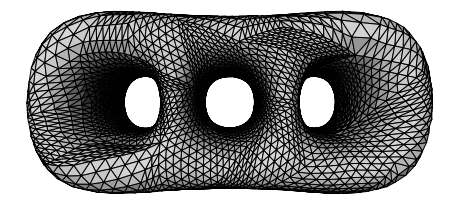
网格卷积

SubDivNet中的一个重要的任务就是完成了将卷积运用到了三维网格这种非结构化的数据中, 由于卷积原本是运用在二维图像这种结构化的数据之上, 所以必须对传统的卷积进行改进, 以便适应三维网格数据。

卷积层的设计

与图像的卷积不同, SubDivNet中设计的卷积只能够对封闭曲面使用, 且卷积之后网格的大小和拓扑关系都不会发生变化, 改变的仅仅是存储在网格面的特征

基础卷积模板

对于一个面$f_i$, 定义它的基础卷积模板为它的1领域邻居, 如下图所示

之后所有卷积核的设计都是在此基础之上做的衍生

卷积核大小

和二维卷积核的定义相似, SubDivNet定义的卷积核的大小也只能用奇数表示。具体而言, 对于一个大小为$k$的的卷积核,那么它的大小是它的所有$1 \ldots \frac{k -1}{2}$领域面之和, 即

$$\Omega(f_i, k) = \bigcup_{i=1}^{\hat{k}}\mathcal{N}_{\hat{k}}(f_i), \hat{k} = \frac{k-1}{2}, k =1,3,5,\ldots$$

下图展示了一个大小为5的卷积核的表示

通过找到其所有1领域和2领域的面来表示这个卷积核

需要注意的是, 当卷积核的大小大于3时, 可能会出现同一个面计算多次的情况, 为了方便, 论文中并没有对这种情况做特殊处理, 并且在设计卷积核的时候通常核的大小不会超过5。

空洞卷积

在设计二维卷积的时候, 有一种常见的设计方法是在计算卷积的时候跳过一些点的计算, 如下图所示

在设计网格的卷积时候, 采用的是一种zig-zag的策略, 简单来说就是不断的通过逆时针-顺时针这样的顺序寻找下一个1领域面, 如下图所示

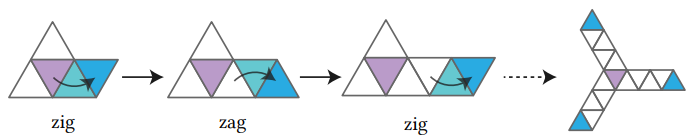
卷积步长

和二维卷积步长不同, 在三维网格中对卷积步长的处理需要用到上述通过remesh建立的网格序列, 假设卷积步长为2, 当前网格($M_l$)是由上一层网格通过1:4的细分得到的, 那么就先找到当前面在上一网格($M_{l-1}$)中的对应, 之后在$M_{l-1}$中找到它的1领域面, 并将1领域面映射回$M_l$, 由于是1:4细分, 所以在$M_l$中有4个面对应, 取中间那个面作为下一个卷积。

一般而言, 如果步长为$s$, 则要求细分的时候采用的是1:$s^2$的细分方式

卷积的计算

不同于图像中的卷积计算, 卷积核的大小始终等于需要训练的参数的个数，在Subdivnet中, 一个卷积核中需要训练的参数始终是4个

之所以和图像中的卷积大不相同, 是因为网格中卷积的计算必须保证和网格面的输入循序无关, 这么做的目的是为了增加网格的鲁棒性, 具体计算方法如下

$$Conv(f_i) = w_0e_i + w_1 \sum_{j=1}^ne_j + w_2 \sum_{j=1}^n \lvert e_{j+1} - e_{j} \rvert + w_3 \sum_{j=1}^n \lvert e_i -e_j \rvert$$

该计算公式适用于$k \geq 3$ 的情况

池化

有了上述remesh的之后, 池化的过程将会变得非常简单, 假设当前网格是$M_l$是通过上一层网格$M_{l-1}$通过$1:s^2$的细分得到的, 池化的作用就是将$M_l$上的特征在$M_{l-1}$上重新表现出来。

由于$M_{l-1}$层中的每一个面片都能在$M_l$上找到$s^2$个对应面片, 与图像中的池化一样, $M_{l-1}$中这个面的特征由这$s^2$个面片的均值或最大值来表示。

下图展示了一个1:4池化的过程

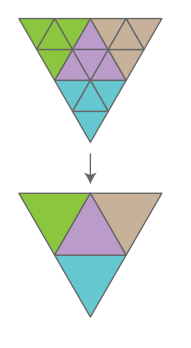
超采样

超采样可以看作是池化的逆过程, 论文中只讨论了使用1:4进行超采样的过程。 假设网格$M_l$通过1:4的方式细分成了网格$M_{l+1}$, 如下图所示,

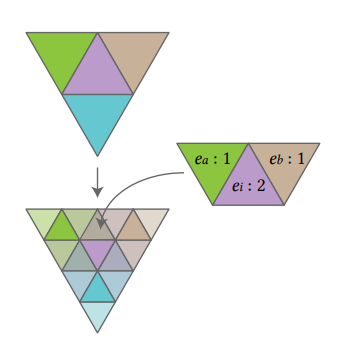
假设面$f_i$被细分成了$\{f_{i1}, f_{i2}, f_{i3}, f_{i4}\}$四个面，其中$f_{i4}$为中心面, 则$f_{i4}$的特征和$f_i$相等, 即$e_{i4} = e_{i}$

假设与$f_{i1}$相邻的两个面分别为$f_{a3}$和$f_{b_1}$, 它们又是由$f_a$和$f_b$细分得到的, 则$f_{i1}$的特征$e_{i1} = \frac{1}{4}e_a + \frac{1}{2}e_i + \frac{1}{4}e_b$

同理可以计算出$f_{i2}$和$f_{i3}$的特征

网络结构

在分类任务中, 网络结构是一个k=1的卷积层, 一个归一化层, 一个ReLu层和一个最大池化层之后再重复该结构1次，即为用于分类的网络结构。

用于语义分割的网络是由resnet50 + deeplab v3+结合而成。

网络的输入

每个面上存储的特征是一个13维的向量, 其中7个维度存放形状信息, 6个维度存放姿态信息。

7个形状信息中1个用来存放三角形面积信息, 3个用来存放三个内角信息, 还有3个用来存放面的法向量与三个顶点法向量的内积。

6个姿态信息中3个用来存放面中点的空间坐标, 3个用来存放面的法向量。

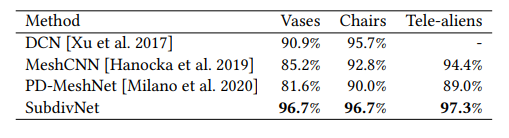
实验结果

分类

数据集

1. SHREC11

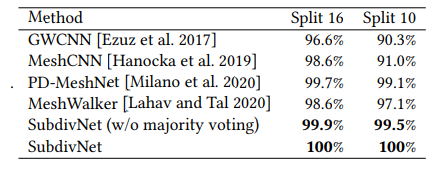
2. Cube Engraving

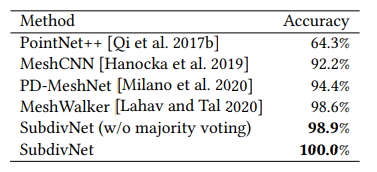
3. Manifold40

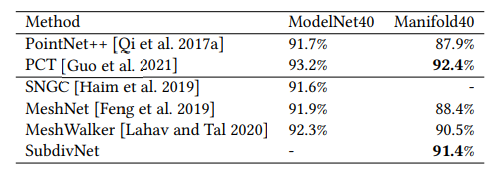
分割

数据集

1. human body

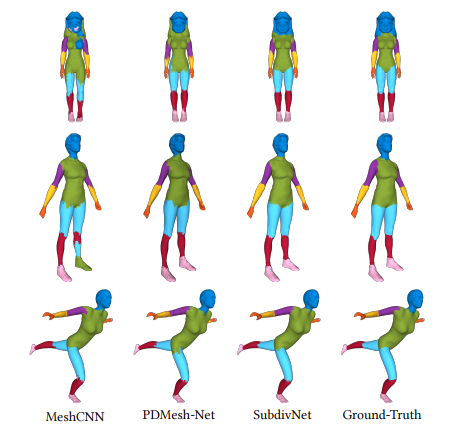
2. coseg